In the past month or two, I’ve spoken on the topic of alert design. There’s a video of my giving the talk (at Monitorama, as well), but I thought I’d try to post on the topic and material as well.
The topic of alerts and “alert design” as seen as a deliberate and purposeful thing to do has been on my mind.
In my experience and my asking many people in engineering and operations (at least in the web and financial trading domains) nothing spikes blood pressure like the topics of alerts. The caricature of the sysadmin waking up to a buzzing pager or phone is what comes to mind.
The costs of not paying attention to how your organization views or treats what comes of this behavior in operational teams (developers and systems folks included) I think are both largely invisible and much higher than most people think. It may be clear that what we’re talking about here is a signal:noise ratio, but it goes way beyond that. The cognitive cost of an engineer to attend to an alert (a fundamentally interrupting event by design) is akin to the cost of a software developer losing their “flow”; context switching is expensive. Expensive from a financial standpoint, a productivity perspective, and I’ll argue a career development view.
Here are some (likely melodramatic) assertions:
- Alert numbness and fatigue is a blight on our industry. Because we can alert on basically anything, and we can argue that anything could be a harbinger of things that could drastically affect our business, we generally put an alert on everything we get our hands on.
- Knowing something has happened almost always trumps not knowing something happened, with sometimes not much effort put into whether the “something” is important with respect to the context it’s happened in.
- Computers deciding what is important to alert on is and will always be brittle. Meaning: alerts and their criteria originate in the author’s mind, which may or may not be in the same place as the receiver of the alert in the future. In other words: we all write documentation and procedures that make sense to us when we write them. They never survive too much of the future, because our worlds that refer to them change. Example: corporate wiki pages are commonly referred to as the place where “documentation goes to die”. Alerts are no different.
Therefore, I’d love to get a much deeper and broader conversation about alert design in our domain. Because I’ll say that it’s not the technology that sucks, it’s our use of it. Consider the possibility that you don’t have a Nagios problem, you have an alert design problem.
Down and In
As the years go by and we see the continued decline of storage prices, the explosion of accessible processing power, we have an ever-expanding ability to zoom in deeply to the ways servers and services talk to each other and process information.
We can zoom in on the relationships and behaviors of seemingly disparate pieces of data, and we can discover and detect disruptions or anomalies in sometimes surprising places. This is interesting, for sure.
But it is also woefully incomplete if we are to make any progress in technical operations.
Up and Out
It is incomplete because as we zoom out of those high-resolution metrics collection and analysis tooling, what we find is a much-ignored environment which includes one of the most powerful context-sensitive and incredibly adaptive anomaly detection and response agents in the world: humans.
Do we have anomaly detection problems? Certainly. One can argue (I will) that we will always have them, for many reasons. (One of those reasons is the Law Of Stretched Systems, but that is for a different post.)
What I’m interested in is not how software can be used to detect anomalies automatically,
(well, I’m interested, but I don’t doubt that we all will continue to get better at it)
…it is how people navigate this boundary between themselves and the machines they work with. The boundary between humans and machines, as we observe our use of tools, is a focus in and of itself. If we have any hope of making progress in monitoring complex systems, we must take this boundary into account.
As an aside, some more bullet points:
- We don’t use a single tool to gain insight into the architectures we build. And we will not, much to the dismay of many monitoring-as-a-service business models. (“A single plane of glass?! Where do I sign?!”)
- Teams of people are the norm, which means that communication and coordination become as important (if not more important) than surfacing anomalies themselves.
- We bring our biases, expectations, trust, and perceptions to the table when it comes to monitoring and response. No tool or piece of automation will ever change that.
- Understanding the breakdowns at these boundaries between people and machines should be a part of how we approach the design of tools. Organizational behavior beats technology at every turn.
Less Code, More Social Science
When we look at Boyd’s OODA loop, we see “observe” and “orient” as critical pieces. Note that these are not Unix commands, they are human activities.
So writing code to tell computers what to look at is quite different than making sure that the code’s human supervisors are equipped or aided in what to look when an alert goes off. Figuring out how people make sense of what is actually going on at a given point (in diagnosis? in planning? in response to an outage? in control?) is just plain hard.
A step that Don Norman (and other folks known in the world of ergonomics and human factors) have been tugging at for a couple of decades is to first attempt to understand how people consume, adapt to, work around, and make use of tools under “normal” operating conditions. Once that’s done, it’s suggested, then we can try to understand how people make sense of their world under high-tempo or escalating scenarios (during an outage, for example) when the signals they receive can sometimes be disorienting as things escalate.
Questions
- Who has ever gotten an alert and ignored it? (/me looks at alert, says “oh, it’ll probably recover, no need to look further”)
- How many alerts were received in the past week that were not actionable? (no human action was required)
- How many alerts were received in the past week as a result of known work being done (expected) but alerts were not silenced during that period?
- How many alerts were received as a result of a previously silenced alert (because work was being done) that was mistakenly un-silenced?
Here are some quotes from engineers who have found themselves in interesting situations related to alerts:
“The whole place just lit up. I mean, all the lights came on. So instead of being able to tell you what went wrong, the lights were absolutely no help at all.”
– Comment by one space controller in mission control after the Apollo 12 spacecraft was struck by lightning (Murray and Cox 1990).
“I would have liked to have thrown away the alarm panel. It wasn’t giving us any useful information.”
– Comment by one operator at the Three Mile Island nuclear power plant to the official inquiry following the TMI accident (Kemeny 1979).
“When the alarm kept going off then we kept shutting it [the device] off [and on] and when the alarm would go off [again], we’d shut it off.”
“… so I just reset it [a device control] to a higher temperature. So I kinda fooled it [the alarm]…”
– Physicians explaining how they respond to a nuisance alarm on a computerized operating room device (Cook, Potter, Woods and McDonald 1991).
“A [computer] program alarm could be triggered by trivial problems that could be ignored altogether. Or it could be triggered by problems that called for an immediate abort [of the lunar landing]. How to decide which was which? It wasn’t enough to memorize what the program alarm numbers stood for, because even within a single number the alarm might signify many different things.
“We wrote ourselves little rules like: ‘If this alarm happens and it only happens once, don’t worry about it. If it happens repeatedly, but other indicators are okay, don’t worry about it.'” And of course, if some alarms happen even once, or if other alarms happen repeatedly and the other indicators are not okay, then they should get the LEM [lunar module] the hell out of there.
– Response to discovery of a set of computer alarms linked to the astronauts displays shortly before the Apollo 11 mission (Murray and Cox 1990).
“1202.” (Astronaut announcing that an alarm buzzer and light had gone off and the code 1202 was indicated on the computer display.)
“What’s a 1202?”
“1202, what’s that?”
“12…1202 alarm.”
– Mission control dialog as the LEM descended to the moon during Apollo 11 (Murray and Cox 1990).
“I know exactly what it [an alarm] is–it’s because the patient has been, hasn’t taken enough breaths or–I’m not sure exactly why.”
– Physician explaining one alarm on a computerized operating room device that commonly occurred at a particular stage of surgery (Cook et al. 1991).
These quotes are from the excellent paper The Alarm Problem and Directed Attention in Dynamic Fault Management (Woods, 1995).
David Woods writes at great length on the topic and gives great insight into what essentially alerts and alarms are: directed attention. As operators of systems that are beyond our full understanding at any given point and perspective, he shines light on the core of the alarm problem: that there is always context sensitivity to alerts, and in many ways the author/designer of the alert hasn’t (can’t!) imagine how the receiver of the alert will interpret it.
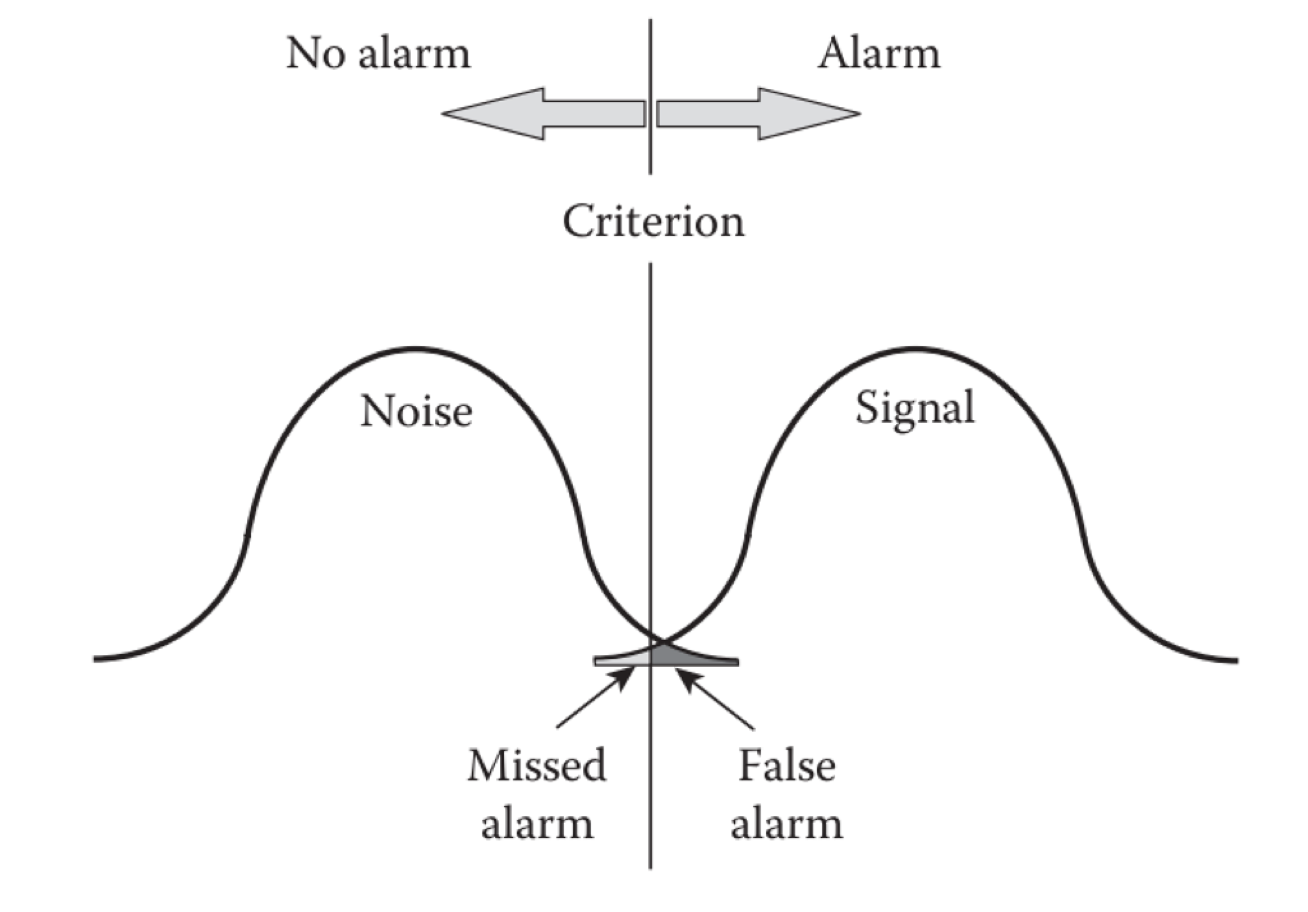
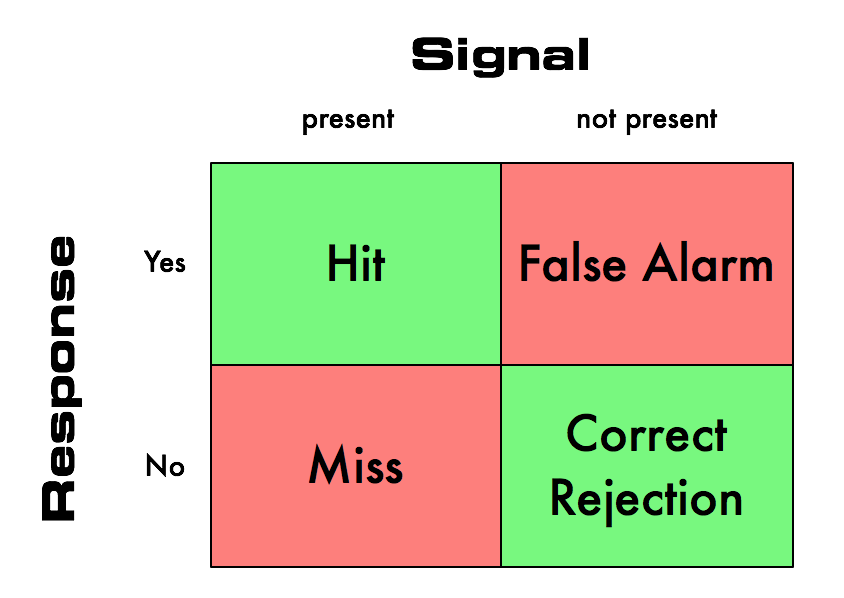
For example: he points to signal detection theory as a framework for thinking about alert/alarm criteria. That is to say, there is always a relationship between true “signal” and “noise” and the trade-offs inherent in choosing the alerting criteria (sometimes, but not always, viewed as a simple threshold) can be thought of like this:
In other words, there are four outcomes that are possible that reflect how sensitive the alerting criteria can be:
So this is a tough one, and points out that getting good (forget about perfect!) signal-to-noise ratio is hard. Too sensitive, you’ll get too many false alarms. Not sensitive enough, and you’ll miss something.
I’ll say that because of this, we generally err on the side of too many false alarms. For fear of missing something (or the embarrassment of it being known that you missed something going wrong with your systems!) we will crank up the sensitivity.
But in doing so, we essentially ignore the detrimental effect of the false alarms on our engineers and organizations. Underlying the false alarms are not just limitations in the alerting algorithms themselves, but the conditions and factors that the alert systems cannot detect or interpret.
An often-given example of this manifests at the Cincinnati Airport. A riverbank leading up to a particular runway there triggers a threshold in ground proximity warning systems (in-cockpit alerts) because the system can’t detect that it’s going to plateau at the runway. Pilots familiar with this particular runway at this particular airport ignore the alerts.
Once more, with feeling: the pilots, who are flying massive cylinders of metal containing many humans ignore a Ground Proximity Warning alert.
When we talk about how the receiver of an alert will behave, we begin to uncover the context sensitivity of an alert.
How can we take into account how someone might react when we they are woken up to an alert we’ve designed? Will they shake their head, wondering what it’s all about? Are we helping them understand what might be going on, or hindering them by including only the bare minimum of data?
What about the engineer who gets an alert in a sea of alerts, while an outage is ongoing? How much attention will they give one amongst a hundred?
Something that might affect our behavior when we get an alert is the amount of trust that we have in the alert: is it telling us something we should believe? Should we drop everything we’re doing in order to pay attention to it? If not, why not?
As an example of this, take the Ground Proximity Warning System I mentioned above. Turns out that in many studies across a number of years, a majority of pilots delay reacting to a GPWS alarm, not just in Cincinnati. Why? Because they take time to validate that the alarm is actually legitimate by looking out the window. This is enough of a problem that the FAA has coined this phenomenon “delayed GPWS response syndrome“.
Trust in automation: it’s a thing that might be worth thinking closely about.
Two Views
“The critical point is that the challenge of fault management lies in sorting through an avalanche of raw data — a data overload problem. This is in contrast to the view that the performance bottleneck is the difficulty of picking up subtle early indications of a fault against the background of a quiescent monitored process.” (Woods, 1995)
The next time you set up an alert in your system, consider how you’re thinking the receiver of that alert will take it. Do you believe that your alert will save the day, providing information for someone to head off catastrophe before it’s too late? Or will it be likely discarded as noise amongst a sea of alerts as someone struggles to understand an outage?
“Information is not a scarce resource, attention is.” – Herb Simon
Herb Simon has mentioned this in many pieces of his writing, as David Woods and Emily Patterson remarks in Can We Ever Escape From Data Overload, A Cognitive Systems Diagnosis. Thus far we’ve captured that designing alerts is hard, even if we only invest effort in capturing signal, forget about providing context. Woods talks a bit more about directed attention, about a paradox:
“Note the paradox at the heart of directed attention. Given that the supervisory agent is loaded by various other task related demands, how does one interpret information about the potential need to switch attentional focus without interrupting or interfering with the tasks or lines of reasoning already under attentional control. We can state this paradox in another way: how can one skillfully ignore a signal that should not shift attention within the current context, without first processing it — in which case it hasn’t been ignored.”
So Where Is “Design”?
“It is the expertise of the human operator that makes it possible to adapt the performance of the joint system, in real time, to unexpected events and disturbances. Every working day, across the whole spectrum of human enterprise, a large number of near-misses are prevented from turning into accidents only because human operators intervene.
The system should therefore be designed so that human adaptation is enhanced.”
(emphasis mine) – Erik Hollnagel, Expertise and Technology: Cognition & Human-Computer Cooperation, 1995
Instead of thinking about alerts and alert design as tasks that underscore the mental model of a subordinate or otherwise dumb messenger delivering news to us?
What if we viewed alerting systems as a partner? What does the world look like if we designed alerting systems to cooperate with us?
If trust in alerting systems is such a big deal, as it is with the GPWS and alert numbness, what can we learn from how humans learn to trust each other, and let that influence our design decisions?
In other words: how can we design alerts that support our efforts to confirm their legitimacy, or our expectations when an alert will fire? Is context-sensitivity part of this?
This is the type of partnership and thinking that I’m interested in. 🙂

As a Junior Systems Administrator in the thick of alerts throughout the day, this article is extremely prescient. The topic itself, however, can turn into a discourse on the erudite and abstract nature of human behavior or situation-specific valuation calls (and more often than not devolves into skull-smashing from more senior personnel).
More often than not, what a manager or stakeholder considers to be a “critical problem” is actually something that can be shunted-off to a logging system such as Splunk or SumoLogic, and easily sliced-and-diced for their respective teams to review and get statistical information on. Operations doesn’t want to know the number of times a customers’ site cache has filled or how often that cache fails to clear.
What we’ve been discussing recently is how to alert properly for given scenarios and how things like Nagios service dependencies would affect our overall stack monitoring. I think the over-arching discussion at this point with most organizations is how to more accurately detect problems and how to show only the urgent problems while simultaneously dropping the “noise” until said problems are resolved.
Otherwise, great article. Thanks.
Pingback: July 2013 Newsletter |Metafor Software
Excellent observations. Part of the challenge in our industry is historic. Ten years ago working in pre-sales for a monitoring vendor it was not uncommon for our tools (and those of competitors) to be judged by just how many out of the box alerts they had. Alerts for everything. Add that to a little lazy thinking where because there was a mechanism for drawing something to a persons attention we used it for everything, rather than thinking about the context in which it needed to be used.
I find that most of the alerts displayed by tools are not about immediately critical issues but rather provide notice that the underlyting system may be in need of a bit of servicing, if they were cars we might call it a tune up. It isn’t critical right now but I might provide benefit if we did it. So comes the challeneg of how to separate real problem indicators from advisories? …
Alerts should be actionable, if you get alerts that are not actionable you are doing yourself and your team a disservice and the alerts will eventually get filtered and ignored. As you design alerts, they should be designed and tweaked constantly. If an alert comes in that you can’t take action on, the alert should be adjusted to have an actionable item. Actionable alerts should also come with as much data as possible to empower the alerted.
I wrote something similar a few years back called “The Philosophy of Monitoring”: http://morgajel.net/2010/06/30/755
Pingback: Counterfactual Thinking, Rules, and The Knight Capital Accident | Kitchen Soap
Pingback: The Importance of Observability - Server Fault Blog
Pingback: M-A-O-L » Owning Attention (Considerations for Alert Design)
Just a quick thought – I think James is onto something when he says this:
“something that can be shunted-off to a logging system such as Splunk or SumoLogic, and easily sliced-and-diced for their respective teams to review and get statistical information on. Operations doesn’t want to know the number of times a customers’ site cache has filled or how often that cache fails to clear.”
A lot of smaller and medium-sized orgs don’t have repositories in place to collect metrics for later analysis. So perhaps in reality (even if we don’t like it) the paging/alerting system takes this on and becomes dual purpose. Sometimes people might want the alert enabled just so they have a record of things later. Often the problem isn’t that we didn’t know what you’re writing about here – the problem is that we live in less-than-ideal operational and business realities.
After all, it seems like a rather large and intimidating project to setup some big repository and get analytics going on it. Saving everything in my email and searching for it later often seems to work well enough… :-/
Pingback: The Importance of Observability - DL-UAT
Pingback: How Etsy Ships Apps – Code as Craft | Artificia Intelligence
Pingback: How Etsy Ships Apps - Code as Craft - Engineering News
Pingback: How Etsy Ships Apps – SRE
Pingback: Developer Experience Lessons Operating a Serverless-like Platform At Netflix — Part II - Engineering News
Pingback: Developer Experience Lessons Operating a Serverless-like Platform At Netflix — Part II – SRE
Pingback: Developer Journey Classes Working a Serverless-esteem Platform At Netflix — Piece II | A1A